MENENTUKAN
NILAI MAKSIMUM dari SUATU FUNGSI PERSAMAAN LINEAR dengan METODE ANALISI SIMPLEKS
Contoh:
Tentukan nilai z jika z = 10x + 15y , dengan
kondisi :
x + y ≤ 16……..(1)
x + 2y ≤ 20…..(2)
x,y ≥ 0
·
Metode
simpleks
z = 10x + 15y
x + y + p = 16……(1a) -> p
sebagai variael yang tidak diproduksi
x + 2y + q = 20….(2a) -> q
sebagai variabel yang tidak diproduksi
·
Keadaan
awal → x = y = 0 , p = 16 , q = 20 , z = 0
·
Pilih
basis
Periksa
ketika ,
Maka q sebagai non basis
·
Selanjutnya
dari 2a
x + 2y + q = 20
2y = 20 – x – q
x + y + p = 16
p = 16 – x – y
t;line-height:
115%;font-family:"Arial Unicode MS","sans-serif"'>2y = 20 – x – q
·
Ketika x =
q = 0 , y = 10 , p = 6 , maka langkah selanjutnya dengan iterassi (pengulangan
untuk x). lihat 2aa dan 1aa.
(
karena tadi udah dikatakan bahwa p dan q merupakan variabel yang tidak
diproduski maka keduanya bernilai 0)
z = 180
contoh :
tentukan nilai z jika z = 2x
+ y , dengan kondissi :
2x + y = 15…..(1)
x + 3y = 20…..(2)
·
Metode
simpleks
z = 2x + y
2x + y + p = 15……(1a) -> p
sebagai variael yang tidak diproduksi
x + 3y + q = 20….(2a) -> q
sebagai variabel yang tidak diproduksi
·
Keadaan
awal → x = y = 0 , p = 15 , q = 20 , z = 0
·
Pilih
basis
Periksa
ketika ,
Maka
p sebagai non basis
·
Selanjutnya
dari 2a
x
+ 3y + q = 20
x
= 20 – 3y – q …..(2aa)
·
Selanjutnya
dari 1a dan subtitusikan nilai x dari 2aa
2x + y + p = 15
p = 15 – 2x – y
p = 15 – 2(20 – 3y – q) – y
p = 15 – 40 + 6y + 2q – y
p = -25 + 5y + 2q….(1aa)
·
Ketika y =
q = 0 , x = 20 , p = -25 , maka langkah selanjutnya dengan iterassi
(pengulangan untuk y). lihat 2aa dan 1aa.
Ketika, x = q = 0 → x = 20 – 3y – q
Maka x mininalnya adalah 5
·
Selanjutnya
didapat
-5y = -25 + 2q – p
(
karena tadi udah dikatakan bahwa p dan q merupakan variabel yang tidak
diproduski maka keduanya bernilai 0)
z = 15

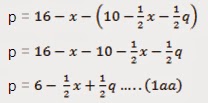






Tidak ada komentar:
Posting Komentar